*하용호님 피피티를 참고하여 정리했습니다.
퍼셉트론(Perceptron)

- inputs: 입력데이터
- weights: 각 입력데이터들에게 주어지는 가중치
- transfer function: 개별 변수(입력데이터)마다 connected되어 표현한 것 = 선형식

- activation function: Neural Network는 분류/예측을 위해 선형식을 사용한다는 것을 알 수 있습니다. 하지만, 대부분의 분류/예측은 선형식의 형태로 이뤄지지 않습니다. 선형식은 예측 및 분류 작업에 있어서 한계를 가집니다. 이런 한계점을 제거하기 위해 activation function을 사용합니다. transfer function을 거친 값이 activation function을 통과하면 선형식에서 비선형식으로 바뀌게 됩니다.

가장 많이 알려진 step function과 sigmoid function의 형태이다. sigmoid function같은 경우 gradient vanishing 문제가 있기 때문에 이를 보완하기 위한 ReLU function을 최근에 많이 사용합니다.
activation을 거친 값은 분류 문제를 진행할 경우 임계값을 기준으로 특정 집단으로 구분된다. 이것이 하나의 퍼셉트론에서 최종 결과물이 됩니다.
activation function의 특징은 1. 연속성 2. 비선형성 3. 단조증가 4. bounded 5. 점근성 다섯가지가 대표적이다. 선형식이 activation의 function으로 들어가면 위의 특성을 가지고 변하게 됩니다.
퍼셉트론을 여러개 사용해서 계속 층을 쌓아나간 것을 Deep Neural Network(DNN)이라고 합니다.


Neural Network의 한계점과 해결방안
1. Underfitting
2. Slow
3. Overfitting
Underfitting
Neural Network의 학습방법은 Backpropagation입니다. 간단히 말하면 현재 내가 틀린정도를 '미분(기울기)'하여 전달하는 것이죠. 미분하고, 곱하고, 더하고를 역방향으로 반복하며 parameter를 업데이트 합니다.
backpropagation에 대해선 다음에 자세히 다루도록 하겠습니다.

여기서 문제가 발생합니다. 예전엔 activation 함수로 sigmoid 함수를 주로 사용했거든요.

sigmoid 함수를 보면 가운데 부분은 미분을 했을 때 특정 값이 나오게 됩니다.

하지만 이 부분의 기울기는 0이 됩니다. 미분 값을 곱해서 역방향으로 전달하는 backpropagation에서 0을 곱해주면 역방향으로 결국 0을 계속 전달해주게 되는 것 입니다.
이걸 Vanishing gradient 문제라고 말합니다. 레이어가 깊어질수록 업데이트가 잘 안되고 결국 underfitting이 일어나는 것이죠.

이를 해결하기 위해 activation함수로 ReLU 함수를 사용합니다.

ReLU 함수를 보면 양의 구간은 전부 특정한 미분 값이 존재하기 때문에 vanishing gradient 문제를 해결할 수 있습니다.
Slow
기존 Neural network는 학습 속도가 매우 느렸습니다. 그 이유 중 하나가 기존 Neural network이 가중치 parameter들을 최적화(optimize)하는 방법으로 Gradient decent 방법을 사용했기 때문입니다. loss function의 현 가중치에서 기울기(gradient)를 구해서 loss를 줄이는 방향으로 업데이트하는 방법인데요, layer가 많아지면 계산량이 높아지고, 중간 layer에서 찾은 최적해가 마지막까지 갔을 땐 최적해가 아니라면 마지막 layer에만 fitting된 값이 될 수 있는 문제점이 있습니다.
Neural network는 loss function(틀린 정도)를 가지고 있습니다. 현재 가진 weight 세팅(내 자리)에서, '내가 가진 데이터를 다 넣으면' 전체 에러가 계산됩니다. 거기서 미분하면 에러를 줄이는 방향을 알 수 있습니다.(내 자리의 기울기 * 반대방향)
그 방향으로 정해진 스텝량(learning rate)을 곱해서 wight를 이동시키고 이 과정을 반복합니다.

하지만 '내가 가진 데이터를 다 넣는다'라는건 보통 사용하는 데이터양을 생각했을 때 불가능에 가깝습니다. 시간이 너무 오래 걸리게 되죠. 그래서 Gradient decent 방법보다 더 빠른 optimizer를 찾게 됩니다. 그게 바로 stochastic gradient decent(SDG) 입니다.
SDG는 느린 완벽보다 조금만 훑어보고 빨리 가자는게 컨셉입니다.
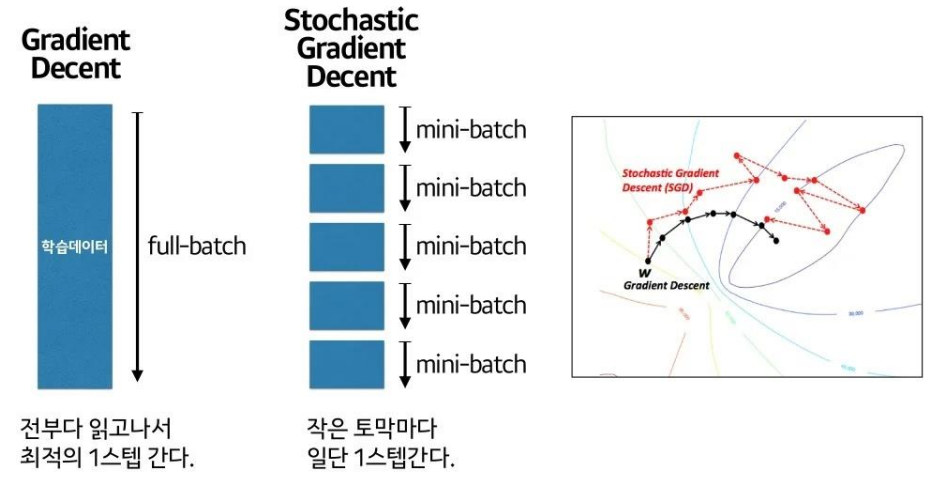
gradient decent에 비해 조금은 헤매지만 빠르게 비슷한 도착지점으로 가게 됩니다.
하지만 미니 배치를 하다 보니 방향성에 문제가 있습니다.

바로 스텝사이즈(learning rate)도 문제가 되는 것이죠. 보폭이 너무 작으면 오래 헤매고, 보폭이 너무 크면 최적값을 그냥 지나치게 됩니다. 어느 방향으로 발을 디딜지, 얼마나 보폭을 크게 할지를 잘 잡아야 합니다.
SDG를 개선하기 위해 많은 optimizer들이 발달되었는데요, 아래 사진에 한번에 정리되어 있습니다.

이 중 최근에 가장 많은 호평을 받고 있는 optimizer는 Adam입니다.
Overfitting

이 사진이 overfitting을 정말 잘 표현 한 것 같은데요, 특정 feture에 너무 알맞게 학습되어 버리면 조금만 달라도 다른 class로 분류하거나 예측해버립니다. 이를 해결하기 위해서 주로 Dropout 방법을 씁니다.

dropout으로 일부에 집착하지 않고 중요한 요소가 무엇인지 터득해 나갈 수 있습니다.
'AI > Machine Learning' 카테고리의 다른 글
| Activation Function(활성화 함수) (0) | 2022.06.23 |
|---|
